열역학 제1법칙은 에너지 보존법칙으로써, 열과 일에 대한 관계를 말해주는 법칙이에요~
먼저 일에 대해서 알아봅시다.
<일(work)>
열역학에서 일은 팽창일과 비팽창일로 나눌 수 있어요.
기체의 부피가 팽창하면서 행하는 팽창일이나, 기체를 압축하는데 필요한 압축일을 PV work라 하고,
전기적인 일이나, 화학적인 일을 비팽창일(non-PV work)이라고 해요.
제가 자주 영어로 말씀드릴 건데, 그건 한국말로는 제대로 전달되지 않거나 의미전달에 혼동이 있을 수 있기 때문에 그래요.
어떤 사람은 비열이나, 비부피, 비엔탈피 처럼 비팽창일을 specific work라고 이해하는 사람도 있거든요.
비팽창일은 건전지, 화학전지 같은 전기화학적인 일을 의미하는겁니다.
자, 그럼 팽창일 PV work에 대해서 살펴봅시다.

힘 F를 가해서 거리 dx만큼 움직였을 때 "일을 했다"라고 얘기 할 수 있어요.
이것을 식으로 표현하면, dW=F*dx로 쓸 수 있어요.
여기서 W는 일이고, F는 힘, dx는 힘을줘서 이동한 거리를 말합니다.
힘F 는 외부압력(Pex) * 단면적(A) 이므로, 기체가 한 일 dW = Pex * A * dx 가 되고,
단면적(A) * dx는 그림에서 보면, 뭐에요?
A*dx는 면적 곱하기 높이니까, 위 그림에서 파란색으로 된 부피를 말하는거에요.
(지금보니까 그림에서 파란색이 좀 더 위로 넓게 그려져야 겠네요)
A곱하기 dx는 dV가 됩니다. 그럼 이 식에서 A*dx는 dV니까, dW=Pex*dV 가 됩니다.
하지만, 화공열역학에서는 일에 대한 미분식을 이렇게 쓰지 않고,
dW = -PexdV라고 써요.
일에 대한 표현이 책마다 다르고, 분야마다 달라서, 아마 혼란스 러워 하시는 분들이 분명히 있을거에요!
정리해드리겠습니다.
이렇게 일에 대한 표현이 다른건 부호에 대한 약속이 서로 다르기 때문에 그런거에요.
화공열역학에서는 부호약속에 따라서 계가 일이나 열을 받으면 (+),
계가 외부로 일을하거나 열을 방출하면 (-)부호를 쓰기로 약속했기 때문에 그런거에요.
계가 일을 한다는 것은 계가 팽창한다는 의미이고, 팽창할 경우에 부피변화 dV는 양수가 되죠?
그래서 dW = PexdV값은 양수가 됩 니다.
그런데 화공열역학에서는 계가 일을 할 때 W는 음수로 약속했기 때문에 dW = -PexdV라고 하는거에요.
앞으로 엄청나게 많이 쓸 공식이니까, 반드시 암기하세요~!
기체의 팽창일의 크기를 계산하기 위해서는 이 식을 적분해서 구할 수가 있는데,
이 식을 적분하기 위해서는 압력(Pex)과 부피(V)와의 관계식을 알아야 해요.
다시 말해서, 등온공정인지, 단열공정인지, 정압공정인지, 가역인지 비가역공정인지,
이상기체인지, 실제기체인지를 알아야지만 이 식(dW = PexdV)을 적분해서 일의 크기를 구할 수 있다는 얘기에요.
<이상기체의 비가역 등온 팽창>

그러면, 이상기체의 등온공정을 가역/비가역 공정에 따라서 살펴 봅시다.
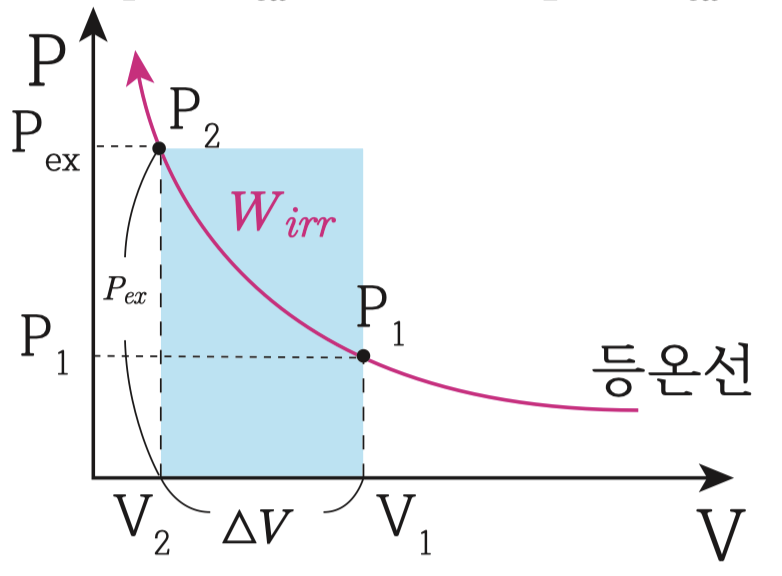
위 그림과 같이, 부피가 V1이고, 압력이 P1인 이상기체가,
외부압력 Pex에 대항해서 V2, P2까지 비가역 등온팽창할 때의 일의 크기를 봅시다.
여기서 이상기체라고 하는 것은 뒤에서 기체 파트에서 자세하게 다루겠지만,
지금은 PV=nRT공식을 따르는 이상적인 기체라고만 알고 넘어갑시다.
그리고 비가역 팽창이라는 것은 급작스러운 팽창이라고 말씀드렸었죠?
등온공정이라고 하는 것은 온도가 일정한 상태에서 변화하는 공정을 말하고요.
그럼, 실린더 안의 이상기체를 우리의 관심사라고 한다면, 이상기체가 시스템, 즉 계가 될거에요.
이 시스템은 등온공정이므로, PV 선도상에 나타내면, 위 그림에서 빨간색 선을 따라서 변화하게 됩니다.. 그게 바로 등온공정이에요.
PV선도에서 등온선, 정압선, 정적선, 단열선 같은 공정을 표시하는 방법은 뒤에서 폴리트로픽공정 다룰 때 설명드릴게요.
지금은 등온선이 이렇게 그려진다는 것과 시스템인 이상기체는 이 등온선을 따라서 변한다는 것만 알아두세요.
그리고 주위, surrounding의 압력은 Pex로 일정하게 유지될거에요.
System의 초기상태는 P1, V1인 이점이고, 최종상태는 P2, V2인 점으로 나타낼 수 있어요.
그리고, 등온공정이므로 등온선을 따라서 움직이다가 시스템의 압력이 외부압력인 Pex와 같아지는 점,
즉 P2에서 기계적 평형을 이루면서 멈추게 될거에요.
여기서 system의 압력이 외부의 압력인 Pex와 평형을 이루는 것을 기계적 평형(mechanical equilibrium)이라고 해요.
이 과정에서의 일의 크기를 계산하려면, 팽창일의 정의 dW = -Pex dV 식을 적분하면,
인테그랄 dW는 인테그랄 -PexdV이고, 인테그랄 dW는 W가 됩니다.
W는 경로함수이기 때문에 적분하면 delta W가 아니고, 그냥 W가 되는거에요,
엄밀하게 얘기하면, 여기서 dW라고 쓰면 안되고, δW로 써야하지만, 스미스책에서도 그냥 dW로 표기하니까 스미스책을 따르도록 할게요.
외부의 압력 Pex는 일정하므로 상수에요. 변하지 않는 숫자라는 얘기에요.
상수는 인테그랄 밖으로 그냥 나올 수 있는겁니다.
그래서 위 식을 적분한 결과가 W=-Pex deltaV가 되는거에요.
델타V는 나중V-초기부피를 뺀 값을 의미하고, 이것을 그래프 상에 나타내면, V2-V1인 이 길이가 ∆V가 되고,
외부의 압력 Pex 는 일정하므로 위 그림 처럼 그려질거에요.
그러면, W = -Pex ∆V는 PV선도에서 파란색 칠해진 면적이 되고, 이 면적의 크기가 바로 팽창일의 크기가 되는거에요.
<이상기체의 비가역 등온압축>
다음은 이상기체의 비가역 등온압축 공정을 봅시다.

실린더 내의 이상기체는 P1, V1에서 외부의 압력 Pex에 의해 급작스럽게 눌려져서 압축되다가,
외부압력과 크기가 같아지는 P2에서 기계적 평형을 이루고 멈추게 될거에요.
이 과정을 PV선도에 나타내면, 우리의 관심사인 시스템은 등온선을 따라서 초기상태에서 최종상태로 압축과정을 거치게 될거에요.
이 때의 압축일의 크기는 W = -Pex ∆V 로 부터 구할 수 있습니다.
∆V는 V2-V1이므로 그래프 상에서 파란 사각형 밑변의 길이를 나타내고,
외부의 압력 Pex는 일정하므로 파란 사각형 윗변의 선으로 그려질거에요.
그래서 압축일 W는 파랑색 사각형의 면적이 되는거에요.
비가역 등온팽창과 등온압축일의 크기를 비교해보면, 팽창일을 이 등온선 아래로 네모난 상자가 그려지고,

압축일은 빨간 등온선 위로 네모난 상자가 그려지는 것을 알 수 있어요.
그러면, 이렇게 급작스러운 팽창과 압축 과정을 여러 단계에 걸친팽창과 압축으로 나눠서 살펴보죠

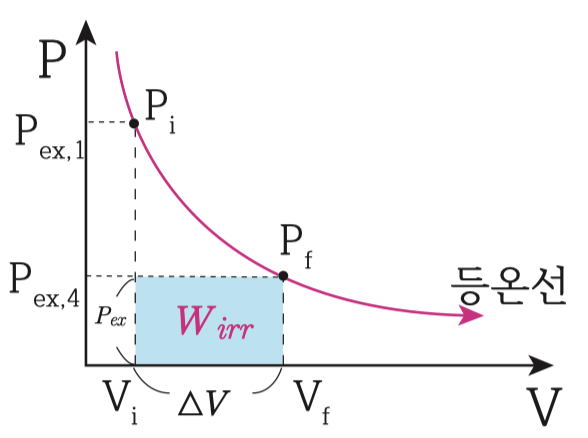
실린더 내의 이상기체의 초기 압력을Pi, 초기 부피를 Vi이라 하고, 최종 압력을 Pf, 최종 부피를 Vf라고 합시다.
그리고 초기상태와 최종상태 사이의 과정을P2, V2, P3, V3라고 할게요.
그리고 각 단계별 외부의 압력을 Pex1, Pex2, Pex3, Pex4라고 한다면,
우측 상단의 그림 원스텝(One step)으로 급작스럽게 비가역적으로 팽창한 경우로써,
계의 부피는 Pi, Vi에서 Pf, Vf로 등온선을 따라서 변하게 될거에요.
그리고 외부의 압력 Pex는 Pex1에서 Pex4상태로 변할거에요.
이 변화 과정에서의 일의 크기를 PV선도에 나타내면 아래 그림과 같이 그려집니다.
피스톤이 여러단계에 걸쳐서 팽창하는 경우를 볼게요.

실린더 내의 이상기체가 초기상태에서 외부압력 Pex3와 같은 크기인 P3 단계를 거치고,
최종단계인 Pf, Vf로 2단계에 걸쳐 팽창하는 경우를 나타낸 그림이에요.
1단계 팽창시 일의 크기는 외부압력 Pex3 * 부피변화 값 V3-Vi가 될거고, 이때의 일의 크기는 빨간색 면적이 될거에요.
2단계 팽창은 외부압력은 Pex4가 되고, 시스템은 V3에서 Vf로 팽창하니까, 일의 크기는 Pex4 *(Vf-V3)가 되겠죠?
이 때의 일 의 크기는 파란색 면적이 될거에요.
다음은, 3단계에 걸친 팽창일을 봅시다.
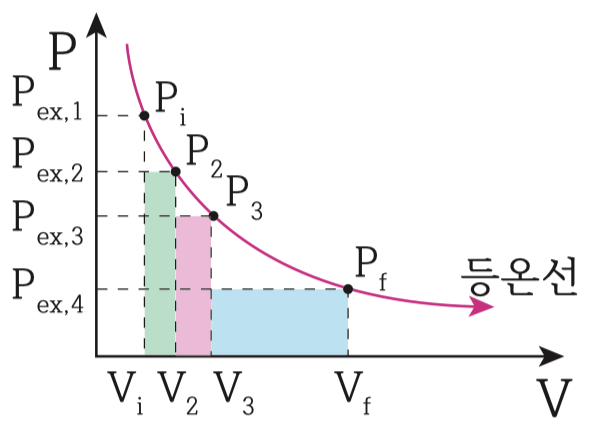
시스템은 초기상태 Pi, Vi에서 P2,V2 --> P3,V3 --> Pf, Vf로 등온팽창 할테고,
이 때의 외부 압력은 Pex1, Pex2, Pex3, Pex4 상태로 변할거에요.
1단계 팽창시 외부압력은 Pex2가 되고 부피변화는 V2-Vi이므로, 일의 크기는 Pex2*(V2-Vi)이 되고,
PV선도상에 나타내면, 일의 크기는 초록색 사각형의 면적이 됩니다.
마찬가지로, 2단계, 3단계 팽창에 대해서 일의 크기를 나타내면 각각 빨간색과 파랑색 면적이 될거에요.
이와 같은 개념을 확대해서, 팽창과정을 아주 작은 무한개의 공정으로 쪼개면,
이것은 가역공정을 의미하고, 아래 그림과 같이 그려질거에요.

이제 원스텝 팽창과, 투스텝 팽창, 쓰리 스텝 팽창, 그리고 무한대 스텝의 팽창 과정에서의 일의 크기인 면적을 비교해 보면,
스텝이 많아질수록 팽창일의 크기가 증가하는 것을 알 수 있어요. 그리고 가역공정일 때 최대의 팽창일을 갖는다는 것도 알 수 있습 니다.
이제 압축공정에 대해서도 똑같이 여러 단계의 스텝으로 쪼개서 봅시다.
원스텝으로 압축될 경우, 초기 상태, 최종상태에요. 외부의 압력은 Pex1에서 Pex4로 압축될거 에요.

외부압력은 Pex4로 일정하게 유지되고, 부피변화는 Vf-Vi, 압축일은 Pex4*(Vf-Vi)가 되므로, PV선도에서는 파란색 사각형 면적이 됩니다.
이 과정을 투스텝으로 쪼개보면, 아래 그림 처럼 돼요.

이 때의 압축일은 첫스텝은 빨간색 면적이 되고, 두번째 스텝은 파 란색 면적이 될거에요.
그리고 다음 그림은 쓰리스텝으로 쪼개면 이렇게 그려집니다.
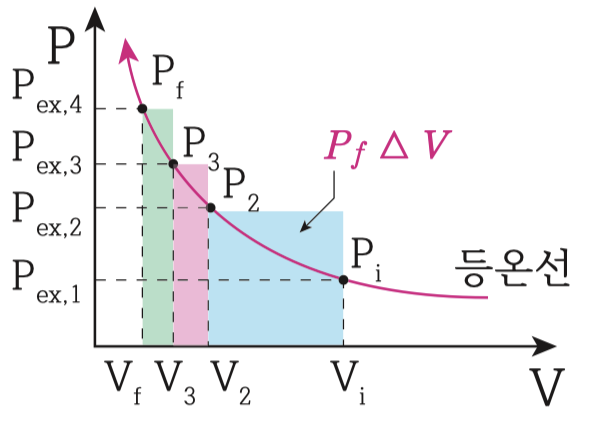
위의 원스텝 과정의 일의 크기와 비교해보면, 압축과정의 단계가 증가 할수록 압축일의 크기가 감소하는 것을 알 수 있죠?
무한대의 스텝으로 쪼개면, 즉 가역공정이 되면, 압축일은 최소가 되는 것을 알 수 있어요.

위에 4개의 그림은 팽창과정을 나타낸 거고, 아래 4개 그림은 압축과정을 나타낸 거에요.
가역일과 비가역일을 비교해 보면, 4가지 특징을 볼 수 있습니다.
| 첫번째, 가역공정의 팽창과 압축은 같은 경로를 따른다. (위 아래의 세번째 그림이 가역팽창 일과 가역 압축일을 나타내는 그림인데, 보시다시피 가역공정의 경우는 팽창과 압축이 같은 경로를 지나는 것 보이죠?) 두번째, 비가역 공정의 팽창과 압축은 서로 다른 경로를 따른다. (위 아래의 첫번째 그림을 비교 해보면 비가역 팽창공정과 비가역 압축공정의 경우 그 경로가 서로 다르죠?) 세번째, 팽창일의 절댓값은 가역공정의 경우가 더 크다. (첫번째 줄 세번째 그림과 첫번째 그림을 비교해보면, 가역공정의 팽창일의 절댓값이 더 큰 것을 알 수 있습니다.) 네번째, 압축일은 비가역 압축공정이 가역 압축공정보다 그 절댓값이 더 크다. (밑에줄 세번째 그림과 첫번째 그림을 비교해 보면, 비가역 압축일 이 더 큰 것을 알 수 있습니다.) |
<가역공정의 순 일(net Work)>
가역공정의 순 일에 대해서 알아봅시다.
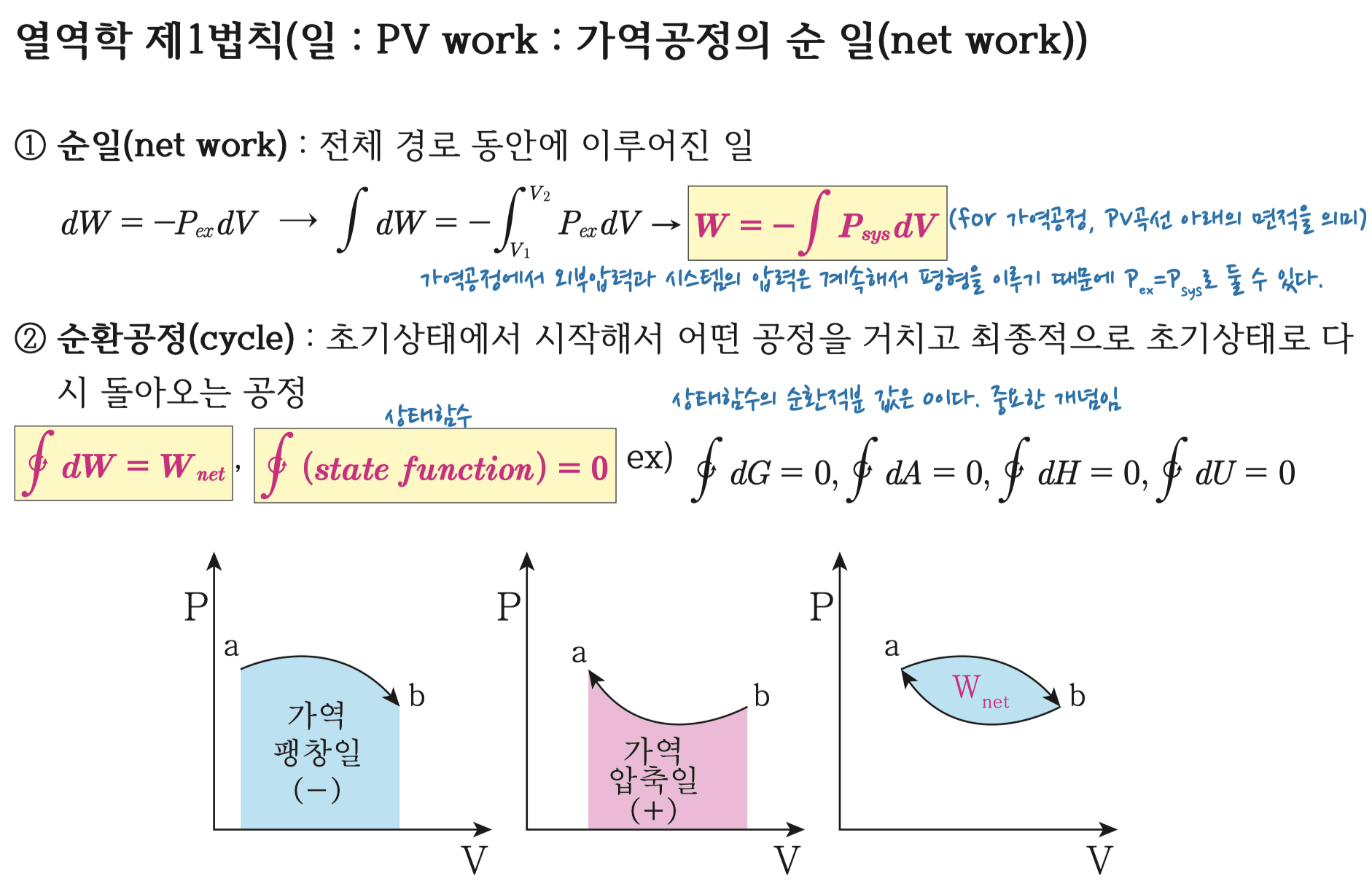
순일, 영어로는 net work라고해요. 순일이라고 하는것은 전체 경로 동안에 이루어진 일을 말해요.
일의 정의로 부터 dW=-PexdV이고, 이를 적분하면, W = - Pex dV 이고,
가역공정일 경우 외부의 압력 Pex는 매 순간순간 계의 압력 Psystem과 같으므로,
위 식은 아래 처럼 바꿔 쓸 수 있게 됩니다.

이 식의 의미는, 아래 그림과 같이 우리의 관심 대상인 시스템이 a에서 b 경로를 따라서 변할 때 적분 면적 이 일의 크기라는 의미에요.

a에서 b로 팽창하는 과정이므로 면적은 팽창일이 되고, 팽창일이니까 마이너스 부호를 갖겠죠?
반대로 b에서 a로 압축되는 이 과정의 적분면적은 압축일이 됩니 다. 압축일이니까 계가 일을 받은 것이므로 플러스 부호를 갖게 될거에요.
그러면, a에서 b로 팽창했다가 b에서 a로 압축되는 순환공정에 대해서 전체 경로 동안에 이루어진 순일 net work는 얼마일까요?
첫번째 그림과 두번째 그림을 더한 그림, 즉 세번째 그림이 의미하는 것이 바로 순일의 크기에요.
정리하면, PV선도에서 어떠한 경로에 대한 적분면적은 일의 크기 를 의미하고, 전체 경로에 대해서 적분한 면적이 순일이라는 의미 입니다.
여기서, 순환 공정에 대해서 한가지 더 짚고 넘어갑시다. 순환공정이라는 것은 사이클(cycle)이라고도 해요.
순환공정, 사이클이라고 하는 것은 초기상태에서 시작해서 어떤 공정을 거치고 최종적으로 초기상태로 다시 돌아오는 공정을 말하는데,
아래 적분기호가 바로 순환공정에 대해서 적분한다는 의미에요.
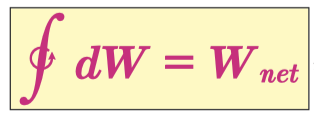
이 의미는 "어떠한 순환공정에 대해서 dW를 적분하면 순일이 된다" 라는 뜻이에요.
그리고, 상태함수는 초기상태와 최종상태에만 의존하는데, 순환공정의 초기상태와 최종상태는 같기 때문에,
이를 적분하면 0이 되는것 은 당연한 사실이에요.
그래서, 상태함수 G, A, H, U를 순환적분하면 그 값은 0이 되는 거에요.
 |
지금까지, 이상기체의 팽창일에 대해서 가역/비가역으로 나눠서 살펴봤는데요,
이렇게 그림으로 분석하는 방법을 도식적인 방법 graphical method라고 해요.
<이상기체의 가역등온 팽창>
다음엔 일의 크기를 구체적인 식으로 나타내고 계산하는 방법을 알아봅시다.
수치적인 해(analytical solution)을 구하기 위해서는 구체적인 P 와 V의 관계식이 필요해요.(아래 그림 참고)

폴리트로픽공정은 $PV^{n}=Constant$ 이고, 등온공정은 PV=Constant, 정적공정은 V=Constant,
정압공정은 P=Const., 단열공정은 $PV^{𝛾}$이 일정하게 변하는 공정이에요.
이런 것들이 PV관계식이에요. 여기 있는 것들은 이상기체에 대해 성립하는 PV관계식이고,
나중에 실제기체의 PV관계식을 배우면 실제기체에 대해서도 일의 크기를 구할 수 있게 됩니다.
그럼, 이상기체, 가역공정, 등온팽창 공정에 대해서 일의 크기를 구해봅시다.
dW=-PexdV이고, 이를 적분하면 $ W=-\int PexdV $
가역공정이니까 외부압력 Pex와 시스템의 압력 Psys가 같아 집니다.
그리고, 시스템은 이상기체이므로, PV=nRT 관계가 성립해요.
P에 대해서 정리하면, $P=\frac{nRT}{V}$ 가 되고, 적분식에 대입하면, $ W=-\int_{V_1}^{V_2}\frac{nRT}{V}dV $
여기서, 이상기체의 몰수 n, 이상기체 상수 R, 절대온도 T는 모두 상수에요(온도는 등온공정이기 때문에 상수)
정리하면,
${\color{Magenta} \displaystyle W=-nRTln\frac{V_2}{V_1}}$
이 식은 이상기체, 가역공정, 등온팽창에 대한 일의 크기를 구하는 식이에요. 유도방법과 결과식 모두 중요합니다.
<이상기체의 가역정압 팽창>

'화공열역학 > 기타(정리중)' 카테고리의 다른 글
| 5. 열역학 제1법칙(열 : 열의 성질) (0) | 2021.08.08 |
|---|---|
| 4. 열역학 제1법칙(일 : 최대 비팽창일 non PV work) (0) | 2021.08.08 |
| 3. 열역학 제1법칙(일 - PV work - PV 관계식 - 폴리트로픽공정) (0) | 2021.08.07 |
| 1. 상태함수, 경로함수, 가역/비가역, 공정, 자발/비자발 개념 (0) | 2021.08.01 |
| 자유도(Degree Of Freedom), 깁스의 상률 (10) | 2018.03.28 |