- 마노미터는 액체 기둥의 높이 차이를 이용해 압력을 측정하는 장치이다.
- 실험실이나 산업 현장에서 비교적 작은 압력 차를 정확하게 측정하는 데 널리 사용된다.
- 기본적으로 투명한 유리 또는 플라스틱 관에 물, 수은, 오일 등 액체를 채워 사용한다.

- 마노미터의 원리는 한쪽에 미지의 압력을 가하고, 다른 한쪽에는 기준 압력(대기압 또는 진공 등)을 가했을 때 두 액체면의 높이 차이가 생기고, 이 높이 차이와 액체의 밀도를 이용해 압력 차를 계산한다.
- 가스의 압력을 $P_1$이라 하고, 대기압을 $P_2$, 마노미터 관 안에 있는 유체의 정지 압력을 $P_3$라 하면, $P_1=P_2+P_3$가 성립한다.
- 유체의 정지압력은 $ΔP=ρgh$이므로 $P_1= P_2 + ρgh$
- 여기서 $ρ$: 액체의 밀도, $g$: 중력가속도, $h$: 마노미터 높이 차
- $P_1$은 절대압이고, $P_2$는 대기압, $P_3$는 게이지압이 된다.
- $P_2$, 유체의 밀도, 유체 기둥의 높이인 h를 측정하면, 탱크 안에 있는 가스의 압력($P_1$)을 계산할 수 있다.
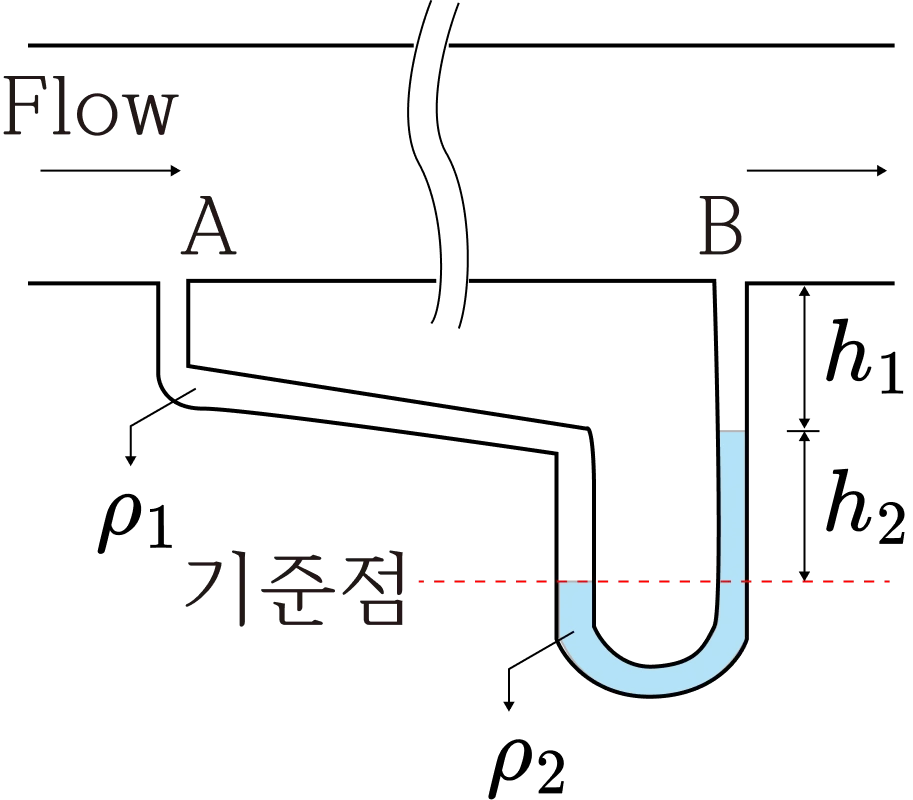
- 두 유체의 밀도가 다를 때는 $(\rho_1 - \rho_2)gh$와 같이 밀도 차를 이용해 압력차를 구한다.
- 기준점에서 유체가 갖는 압력은 서로 같으므로, $P_A + \rho_1 g (h_1 + h_2) = P_B + \rho_1 g h_1 + \rho_2 g h_2$
- $P_B = P_A + \rho_1 g (h_1 + h_2) - \rho_1 g h_1 - \rho_2 g h_2 = P_A + \rho_1 g h_2 - \rho_2 g h_2 = P_A + (\rho_1 - \rho_2) g h_2$
'화공열역학 > Chapter 1. 열역학 기본개념' 카테고리의 다른 글
| Chapter 1-11. 열역학적 성질의 변화( 상태함수, 경로함수) (0) | 2026.01.01 |
|---|---|
| Chapter 1-10. 세기성질(압력: 환산인자) (0) | 2026.01.01 |
| Chapter 1-8. 압력( 절대압, 게이지압, 대기압, 진공압) (0) | 2026.01.01 |
| Chapter 1-7. 세기성질(압력 : 토리첼리의 실험) (0) | 2026.01.01 |
| Chapter 1-6. 열역학적 성질(세기성질: 온도) (0) | 2025.12.31 |